تحلیل تکنیکال با تئوری امواج الیوت، تلاشی برای کشف نظم زیربنایی در حرکات بهظاهر آشفته قیمتها است. این نظریه بر پایهی مجموعهای از قواعد دقیق و مشخص استوار است که انضباط فکری لازم برای تحلیل درست را به معاملهگر القا میکند. در واقع، این قوانین موج شماری الیوت هستند که اساس نظریه الیوت را شکل داده و آن را از سایر روشهای تحلیلی متمایز میسازند؛ زیرا نقض هر یک از این قواعد به معنای باطل بودن شمارش و نیاز به تجدید نظر کامل در الگوی بازار است.
قوانین سهگانه اصلی و خدشهناپذیر امواج جنبشی
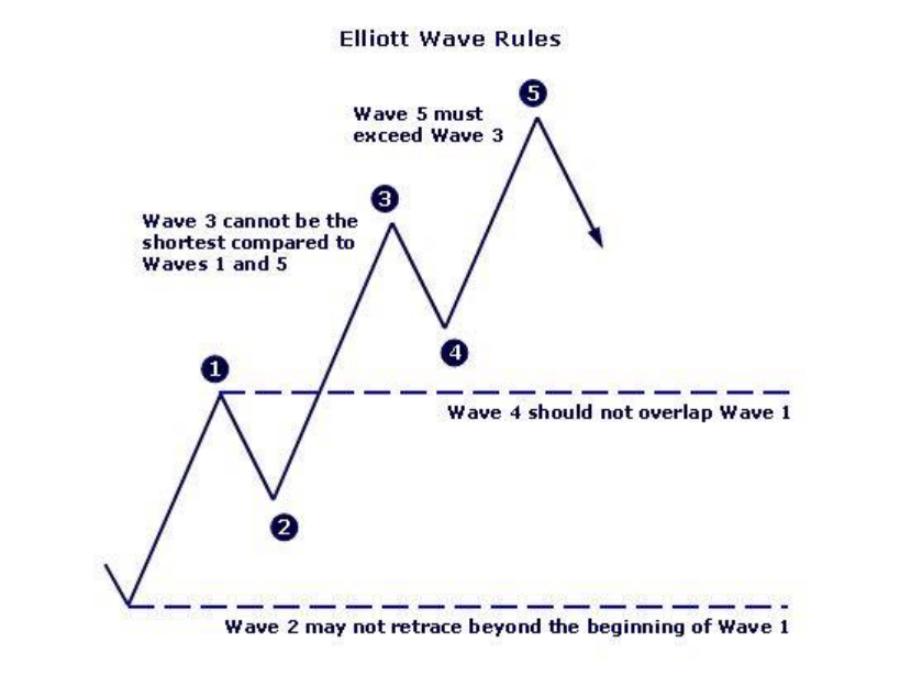
هر الگوی امواج الیوت بر مبنای سه قانون اصلی بنا شده است که در هیچ شرایطی نباید نقض شوند. این قوانین الیوت، اعتبار و صحت شمارش امواج جنبشی (Impulse Waves) را تضمین میکنند و به عنوان یک اصل در این تئوری شناخته میشوند.
قانون اول: اصلاح موج ۲
موج اصلاحی دوم (Wave 2) هرگز نمیتواند بیش از ۱۰۰ درصد موج جنبشی اول (Wave 1) را بازگشت کند. این بدان معناست که انتهای موج ۲ نباید به زیر نقطه شروع موج ۱ برسد، در غیر این صورت، ساختار جنبشی فعلی باطل است.
قانون دوم: اندازه موج ۳
موج جنبشی سوم (Wave 3) هرگز نباید کوتاهترین موج در میان امواج جنبشی (امواج ۱، ۳ و ۵) باشد. موج ۳ اغلب قویترین و بلندترین موج چرخه است.
قانون سوم: محدوده همپوشانی موج ۴ و موج ۱
موج اصلاحی چهارم (Wave 4) نباید وارد محدوده قیمتی موج جنبشی اول (Wave 1) شود. این قانون یک ممنوعیت مطلق در امواج جنبشی استاندارد (Impulse) است و تنها در الگوهای مورب (Diagonals) استثنا وجود دارد.
اصول راهنما و دستورالعملهای امواج جنبشی (Motive Waves)
در قوانین موج شماری الیوت، اصولی برای راهنمایی نیز وجود دارند که گرایش به وقوع دارند، اما نقض آنها ساختار موج را باطل نمیکند. این دستورالعملها به تحلیلگر کمک میکنند تا از میان شمارشهای ممکن، محتملترین سناریو را انتخاب کند.
اصل کشیدگی (Extension) و محلهای معمول آن
در یک الگوی پنج موجی، معمولاً یکی از امواج جنبشی (موج ۱، ۳ یا ۵) به صورت کشیده درآمده و از نظر طول و پیچیدگی از دو موج دیگر فراتر میرود. این کشیدگی در واقع یک ساختار ۵ موجی فرعی در داخل موج اصلی است و موج ۳ شایعترین محلی است که این پدیده در آن رخ میدهد.
اصل تناوب (Alternation) بین امواج ۲ و ۴ اصل تناوب بیان میکند که دو موج اصلاحی متوالی در یک الگوی جنبشی (موج ۲ و موج ۴) باید از نظر شکل و پیچیدگی با یکدیگر متفاوت باشند. برای مثال، اگر موج ۲ یک اصلاح ساده (مانند زیگزاگ) باشد، انتظار میرود موج ۴ یک اصلاح پیچیده (مانند فلت یا مثلث) باشد و بالعکس.
قانون برابری تقریبی موج ۱ و ۵ (در صورت کشیدگی موج ۳) هنگامی که موج ۳ به شکل کشیده درآمده باشد، این گرایش وجود دارد که امواج ۱ و ۵ از نظر طول یا زمان به طور تقریبی با هم برابر باشند، یا اینکه موج ۵ با یکی از نسبتهای اصلی فیبوناچی از طول موج ۱ مرتبط شود. این اصل یک راهنما برای تعیین هدف قیمتی موج ۵ است.
اهمیت آموزش و تسلط بر قوانین موج شماری الیوت
تسلط کامل بر اصول و قوانین الیوت به صورت جزء به جزء، تنها از طریق آموزش ساختاریافته و تمرین مستمر ممکن است. برای اینکه بتوانید این قواعد را به درستی در نمودارهای واقعی به کار ببندید و شمارشهای معتبر انجام دهید، نیاز به یادگیری عمیق دارید. در آموزش امواج الیوت به صورت کامل، تمامی نکات لازم از جمله شناسایی الگوها، تکنیکهای کانالکشی و نسبتهای فیبوناچی به شما آموزش داده میشود تا به یک تحلیلگر مسلط تبدیل شوید.
قوانین امواج اصلاحی
امواج اصلاحی، که در خلاف جهت روند اصلی حرکت میکنند، از پیچیدگی بیشتری برخوردارند و بیشتر بر الگوهای ساختاری و ارتباطات درونی موجها تأکید دارند. این امواج از ساختار سهموجی (A-B-C) در قالبهای مختلف پیروی میکنند.
قانون ساختاری زیگزاگ، فلت، مثلث، همپوشانی امواج اصلاحی میتوانند اشکال گوناگونی مانند زیگزاگ (ساختار 5-3-5)، فلت (ساختار 3-3-5)، یا مثلث (ساختار 3-3-3-3-3) به خود بگیرند. در امواج اصلاحی، به خصوص در مثلثها و الگوهای پیچیده، همپوشانی زیرموجها مجاز شمرده میشود که در امواج جنبشی ممنوع است.
قواعد ساختار زیگزاگ و فلت در زیگزاگ، موج B کوتاهترین است و نباید بیش از ۷۵ درصد موج A را اصلاح کند، و موج C همواره از انتهای موج A فراتر میرود. در مقابل، در الگوی فلت، موج B تقریباً به اندازه موج A یا کمی بیشتر اصلاح میکند و نشاندهنده فشردگی و توقف در حرکت بازار است.
ساختار و نسبتهای داخلی امواج اصلاحی (جزئیات تکمیلی)
امواج اصلاحی (A-B-C) هرچند در ظاهر ساده هستند، اما از نظر ساختار داخلی (Sub-Waves) و همچنین از حیث نسبتهای فیبوناچی بین زیرموجهایشان (A، B و C) دارای قواعد بسیار دقیقی هستند. رعایت این نسبتها، تأییدی قوی بر صحت شمارش الگوهای زیگزاگ، فلت و مثلث در حال شکلگیری است.
ساختار داخلی الگوی زیگزاگ (Zigzag Structure)
ساختار اصلی این الگو بهصورت 5-3-5 است.
-
موج A: همواره یک موج انگیزشی 5 موجی یا یک موج مورب (Diagonal) است.
-
موج B: یک موج 3 موجی است (مانند زیگزاگ، فلت یا مثلث) و نباید بیش از 75% موج A را اصلاح کند.
-
موج C: همواره یک موج انگیزشی 5 موجی یا یک موج مورب است و غالباً از انتهای موج A فراتر میرود.
ساختار داخلی الگوی فلت (Flat Structure)
ساختار اصلی این الگو بهصورت 3-3-5 است و نشاندهنده تعادل نیروها و فشردگی در بازار است.
-
موج B: به عنوان وجه تمایز این الگو، حداقل 90% موج A را اصلاح میکند (و گاهی میتواند تا 100% تا 138% آن را نیز بازگشت کند).
-
موج C: یک موج 5 موجی انگیزشی است.
-
توجه: موج A در یک فلت استاندارد هرگز نباید یک مثلث باشد.
ساختار داخلی الگوی مثلث (Triangle Structure)
ساختار اصلی این الگو بهصورت 3-3-3-3-3 (پنج زیرموج A-B-C-D-E) است که معمولاً به صورت زیگزاگهای متوالی هستند.
-
قانون همپوشانی مثلث: هر موج داخلی نباید از ابتدای موج قبلی خود فراتر رود (مثلاً انتهای موج C به زیر انتهای موج A نمیرسد).
-
عمق اصلاح: معمولاً اصلاح داخلی موج C عمیقتر از دیگر امواج مثلث است.
قوانین کانالکشی و نسبتهای فیبوناچی در تئوری امواج الیوت
کانالکشی و نسبتهای فیبوناچی ابزارهای جداییناپذیری هستند که به تحلیلگر کمک میکنند تا اهداف قیمتی و زمانی امواج را با دقت بالا مشخص کند.
قوانین کانالکشی امواج جنبشی برای تعیین هدف احتمالی موج ۵، معمولاً یک خط روند از انتهای موج ۱ به انتهای موج ۳ رسم شده و یک خط موازی از انتهای موج ۲ ترسیم میشود. موج ۵ غالباً در نزدیکی این خط موازی به پایان میرسد.
نسبتهای فیبوناچی در امواج اصلاحی و جنبشی نسبتهای فیبوناچی برای تعیین عمق اصلاح و اهداف جنبشی ضروری هستند. به عنوان مثال، موج ۲ معمولاً بین ۳۸.۲٪ تا ۶۱.۸٪ از موج ۱ را اصلاح میکند. همچنین، طول موج ۳ و ۵ اغلب به صورت نسبتهایی مانند ۱.۶۱۸ یا ۰.۶۱۸ از طول موجهای قبلی تعیین میشوند.
تفاوت قوانین موج شماری الیوت کلاسیک با نئو ویو
تئوری نئو ویو (NeoWave) که توسط گلن نیلی توسعه داده شده، یک بسط و اصلاح پیشرفتهتر از الیوت کلاسیک است که با هدف رفع ابهامات و افزایش دقت در شمارش امواج، قوانین سختگیرانهتر و متفاوتی را معرفی میکند.
مهمترین تفاوت میان این دو مکتب، در قانون همپوشانی موج ۴ و موج ۱ است. در حالی که الیوت کلاسیک این همپوشانی را در امواج جنبشی استاندارد (Impulse) ممنوعیت مطلق میداند، نئو ویو این قانون را حذف کرده و اجازه میدهد که موج ۴ وارد محدوده قیمتی موج ۱ شود. این تغییر، انعطافپذیری بیشتری به تحلیلگر میدهد و الگوهای بیشتری را معتبر میشمارد، به شرطی که سایر قوانین سختگیرانه نئو ویو، به ویژه اصل تناوب بین امواج ۲ و ۴، رعایت شوند. به طور کلی، نئو ویو قوانین بسیار دقیقتری را برای ساختار داخلی و نسبتهای زمانی امواج اصلاحی وضع میکند که آن را از سادگی نسبی الیوت کلاسیک متمایز میسازد.
سایر قوانین و اصول کلیدی نئو ویو:
- قانون خنثی بودن (Neutrality Rule): این قانون بر اهمیت ارتباطات زمانی بین امواج تأکید دارد و تعیین میکند که یک موج تا چه زمانی میتواند ادامه یابد بدون اینکه شمارش فعلی باطل شود. این قانون، بعد زمان را به شکلی بسیار دقیقتر از الیوت کلاسیک وارد تحلیل میکند.
- قانون پیچیدگی (Complexity Rule): نئو ویو بر این اصل تأکید دارد که امواج اصلاحی بعدی در یک الگو، باید از نظر ساختار پیچیدهتر یا برابر با امواج اصلاحی قبلی باشند. این قانون، اصل تناوب را به یک قانون سختگیرانه و قابل اندازهگیری تبدیل میکند.
- قانون برابری زمانی (Time Equality): در نئو ویو، قوانین سختگیرانهای برای برابری زمانی بین امواج ۱ و ۵ (در صورت کشیدگی موج ۳) و همچنین بین امواج اصلاحی ۲ و ۴ وجود دارد که به تعیین اهداف زمانی کمک شایانی میکند.
- قوانین سختگیرانه برای امواج اصلاحی: نئو ویو قوانین بسیار دقیقی برای ساختار داخلی الگوهای اصلاحی مانند فلتها (Flats) و زیگزاگها (Zigzags) وضع میکند، به طوری که هر زیرموج (A، B، C) باید از قوانین خاصی پیروی کند تا کل الگو معتبر باشد.
- قانون کانالکشی (Channeling Rule): نئو ویو روشهای کانالکشی را به شکل بسیار دقیقتری تعریف میکند و از آن برای تأیید اعتبار یک شمارش و تعیین پایان احتمالی موج ۵ استفاده میکند.
جمعبندی: اهمیت انضباط در قوانین موج شماری الیوت
تئوری امواج الیوت بیش از آنکه یک ابزار پیشبینی باشد، یک چارچوب ساختاری برای سازماندهی اطلاعات بازار است. موفقیت در بهکارگیری این روش، مستلزم پایبندی بیکموکاست به قوانین موج شماری الیوت، بهویژه سه قانون اصلی، و همچنین درک ظرایف اصول راهنما است. این انضباط، تحلیلگر را قادر میسازد تا تفاسیر ذهنی را کنار گذاشته و با تکیه بر ساختار ریاضیاتی و فرکتالی بازار، به شمارشهای معتبر و استراتژیهای معاملاتی موفق دست یابد.
بیشتر بخوانید:

















